Tenis – kto wygra – analityka gry

Tenis – kto wygra – analityka gry. Tenis, podobnie jak inne sporty, ma specyficzny system punktacji. Zdobyte punty dzielone są na podzbiory, gemy. Te fragmenty mają znaczenie dla całego meczu, a nie mają znaczenia dla każdego pojedynczego punktu. Pojawia się więc pytanie: „Jaki jest związek pomiędzy wygrywaniem danego punktu a prawdopodobieństwem wygrania gema, setu i ostatecznie meczu tenisowego?”

Punkty w tenisie jako zmienna, p

Aby uprościć sprawę, załóżmy, że punkt można w pełni opisać tylko jedną zmienną: P, która oznacza prawdopodobieństwo, na ile ten, kto serwuje wygra dany punkt. Np. dla gracza A może to być 60%, bo taka jest statystyka jego dotychczasowych spotkań, a dla gracza B – 30%, co wynika z jego statystyki. Można też założyć, że zmienne te pozostają jednakowe przez cały mecz. Tak więc nie wpływa na nie, wynik poprzedniego punktu, zmęczenie postępujące w czasie ani nic innego.

Gra w tenisa – punktowanie

Tenis jest wyjątkową grą, bo nie każdy punkt ma takie samo znaczenie. Mecz nie jest po prostu wyścigiem o około 150 punktów. Zamiast tego punkty są dzielone na gry – gemy i sety, w których jeden z graczy ma przewagę.

Gra w tenisa – symulacja

Przeprowadżmy prostą symulację, gdzie:

• P oznacza prawdopodobieństwo, że serwujący wygra punkt
• zatem (1-p) oznacza prawdopodobieństwo, że osoba returnująca wygra punkt

Na tej podstawie możemy wygenerować następujący scenariusz gry w tenisa

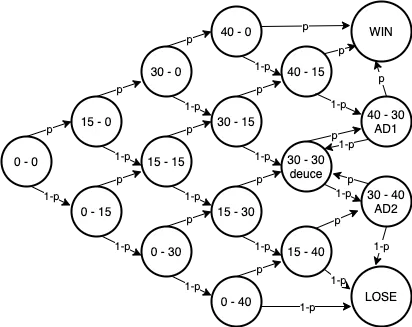
Grę zacznamy od wyniku 0–0, z prawdopodobieństwem P, że osoba serwująca wygrywa punkt. Tak wiec przesuwamy się „w górę” na wykresie. Osoba returnująca przesuwa się „w dół” z prawdopodobieństwem (P-1). Jeśli na końcu gry, jeśli dojdziemy do rozgrywki na równowagi, to mamy pętlę, w której jeden z graczy musi wygrać 2 punkty z rzędu. Widzimy też, że aby wygrać gem w najprostrzy sposów tzeba wygrać 4 punkty z rzedu, to jest 0-15-30-40-wygrana. Prawdopodobieństwo takiego zdarzenia wynosi (p x p x p x p).

Można zapisac równanie P(x;n,p) = P(X=x) = (n nad x)p^x (1-p)^n-x, gdzie n oznacza iloma punktami zagramy, a x to ta wgrana gra. (n nad x) to współczynnik dwumianowy = n!/(x!(n-x)!

Przykład: Jeśli wygrywany do 15, to mamy 5 punktów w grze, wiec n=5 a wygrana x=4. Jeśli jednak, serwujący wgra w 4 punktach to już jest konic gry. W takim przypadku wzór na wgranie gry=gema przez osobę serwująca powinien wyglądać następująco: p_g = p_g(4,0)+p_g(4,1)+p_g(4,2)+p_g(3,3)*suma(p_g(n+2,n). Oznacza to, że prawdopodobieństwo wygranej powinno być rozpatrywane w różnych wariantach. Np. prawdopodobieństwo wygrania (40,0) wynosi p⁴, (40,15) wynosi 4p⁴(1-p), a (40,30) wynosi 10p⁴(1-p)².

Czytaj dalej tutaj (https://towardsdatascience.com/building-a-tennis-match-simulator-in-python-3add9af6bebe)