Biłgoraj - Zalew Bojary - pływanie 100 km

Damian Błaszczyk będzie pływał w Zalewie Bojary, stawiając sobie za cel pokonanie 100 km. Biłgoraj – Zalew Bojary – pływanie 100 km. Przygotowaliśmy zadanie matematyczne jak może wyglądać takie pływanie i w jaki sposób pokonać 100km. Rozwiązanie zadania w dalszej części artykułu.

Cel tego wydarzenia

Ośrodek Sportu i Rekreacji w Biłgoraju “Na Fali” ma zaszczyt zaprosić na wyjątkowe wydarzenie, które po raz drugi zjednoczy nas wokół szczytnego celu! W dniach 25-27 lipca 2025 roku Zalew Bojary w Biłgoraju stanie się areną drugiej edycji akcji “Na Fali Nadziei – Przekraczając Granice”! – czytaj tutaj

W tym roku wspieramy Adasia Iwanejko, 12-latka z Woli Małej, który dzielnie walczy ze śmiertelną dystrofią mięśniową Duchenne’a. Jego jedyną szansą na powrót do zdrowia jest kosztowna terapia genowa w USA, której szacunkowy koszt przekracza 16 milionów złotych. Wierzymy, że dzięki wspólnej mobilizacji możemy zdziałać cuda i pomóc Adasiowi spełnić marzenie o normalnym życiu!

Zadanie 1. Biłgoraj – Zalew Bojary – pływanie 100 km

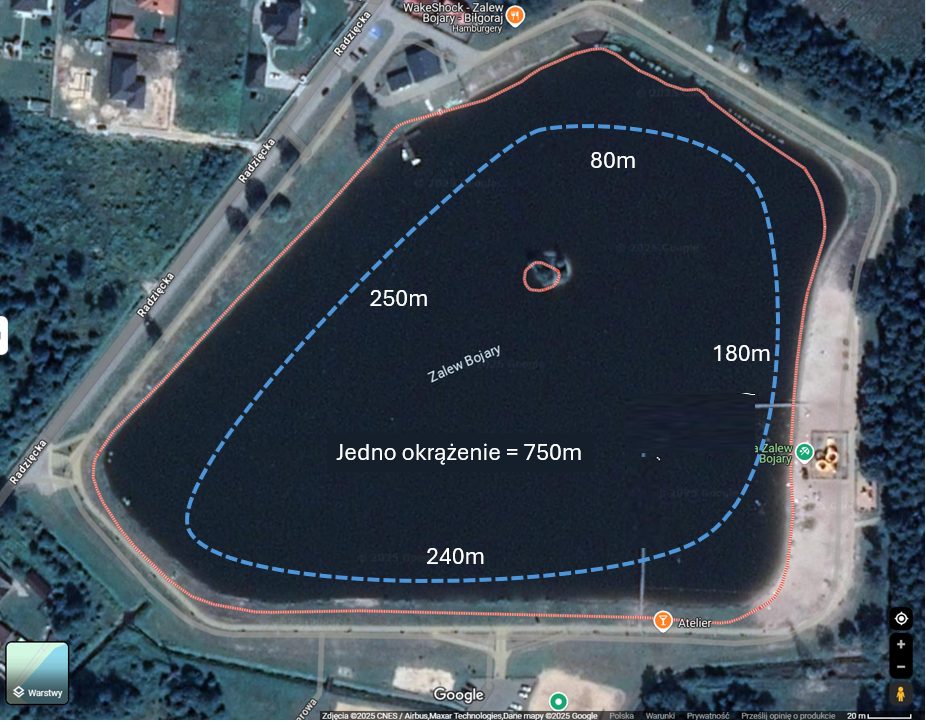
Pływak Damian Błaszczyk ma pokonać dystans 100 km pływając po okręgu przywiązany na linie o długości 100m do słupa o nieistotnej grubości. Lina obraca się wokół słupa zachowująć cały czas długość 100m. Zadanie to jest do wykonania na zalewie Bojary ponieważ zalew ten ma średnicę około 230m. Tak więc zakładamy, że pływak będzie okrążał zalew aż pokona dystans D=100km. Pytanie jest ile okrążeń musi wykonać pływak?

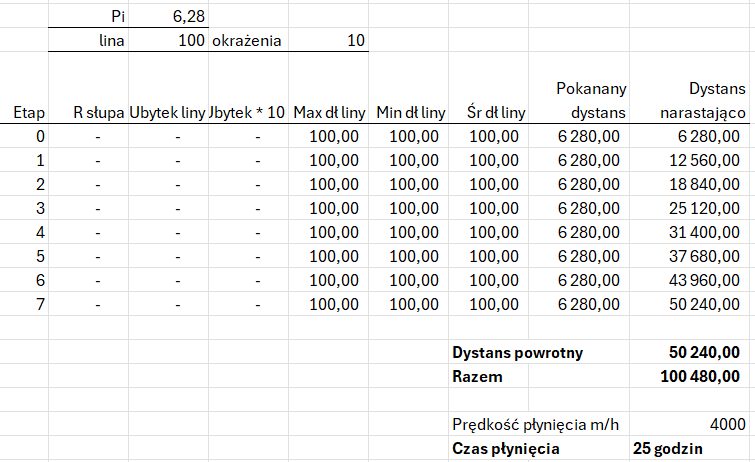
Obliczenia przedstawiono w tabeli poniżej. Pływak wykona 8 rund po 10 okrążeń w prawo, co daje 80 okrążeń i 80 okrążeń w lewo, co daje razem 160 okrążeń. Każde okrążenie daje dystans d=2Pir = 628 m. Tak więc jedna runda 10 okrążeń daje 6,280 m, 8 rund to 50,240 m. Przepłynięcie 100 km wymaga więc 16 rund czyli 160 okrążeń zalewu. Płynąc w tempie 4 km/h zajmuje czas około 25 godzin. W informacji prasowej jest wzmianka, że pływak zamierza pływać 48 godzin, więc jest to realny czas na pokonanie dystansu 100 km. Biłgoraj – Zalew Bojary – pływanie 100 km

Czas potrzebny na pokonanie dystansu 100 km obliczamy ze wzoru: t = d/v, gdzie d=dystans 100 km, a v=prędkość 4 km/godz. Przepłynięcie 100 km w tempie 4 km/h zajmuje czas około 25 godzin. Około oznacza to, że prędkość pływaka może być nieco większa lub mniejsza, wtedy ten czas ulegnie zmianie.

Zadanie 2

Teraz zakładamy, że średnicy słupa wynosi 20 cm, co jest bardziej realne. Lina nawija się na słup w ten sposób, że po każdych 10 ciu okrążeniach przeskakuje na kolejną warstwę zwiększając tym samym średnicę słupa. Pytanie: ile okrążeń musi wykonać pływak aby pokonać dystans 100 km? Biłgoraj – Zalew Bojary – pływanie 100 km.

Rozwiązanie zadania:

Długość początkowa liny = promień początkowy okręgu = 100 m.
Średnica liny = 1 cm ( rl = 0,01 m).
Średnica słupa = 20 cm (promień słupa = 10cm = r0 = 0,1m).

Etap 1, Pływak w pierwszym okrążeniu pokona dystans d = 2Pir = 628 m. W czasie tego okrążenia lina nawinie się na słup, co spowoduje, że jej długość zmniejszy się o d0 = 2Pi * r0 = 0,628 m. Tak więc drugie okrążenie będzie miało długość 628 m – 0,628 m = 627,2 m. Itd aż do 10-tego okrążenia. Czyli w okrążeniach 1-10, lina skraca się o d0 = 2*Pi*r0 = 6.28 * 0,1m = 0,628 m per okrążenie, czyli razem skróci się o 6,28m. Po 10 okrążeniach lina przeskakuje na wierzch poprzednio nawiniętej warstwy, co zwiększa promień słupa o grubość liny, czyli o 1 cm (0,01 m). Tak więc w okrążeniach 11-20, lina skraca się o d2 = 2 Pi * (r0+rl) = 6.28 * 0,11 m = 0,69 m.

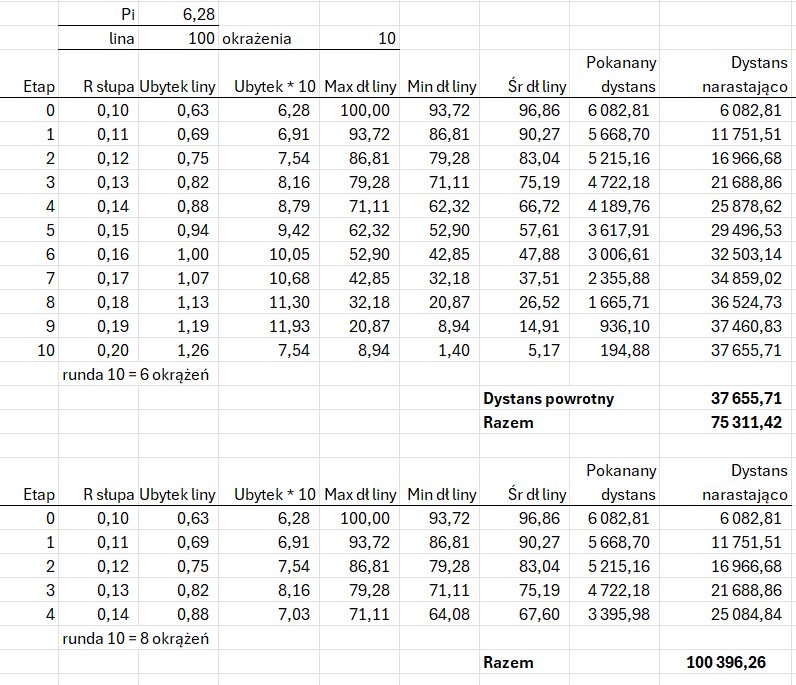
Biłgoraj - Zalew Bojary - pływanie 100 km

Całość obliczeń przedstawia tabela poniżej. Pływak bedzie płynął na coraz to krótszej linie, co spowoduje, że ostatecznie cała lina zawinie się na słup. Po ilu okrążeniach to nastąpi i jaki dystans pływak pokona w tym czasie?

Jeśli pierwsze 10 okrążeń skraca line o 6,28, drugie 10 okrążeń skraca linę o 6,91 m itd. – patrz kolumnę czwartą Ubytek*10, to 100 m liny wystarczy na 10 rund (etapów) po 10 okrążeń i 11 rundę 6 okrążeń. Razem będzie to 106 okrążeń. Da to dystans 37,655 m. Jeśli pływak płynął w prawo to teraz powinien płynąć w lewo, co da kolejne 37,655 m. Ciągle nie będzie to pełne 100 km. Potrzebne są jeszcze 4 rundy o 8 okrążeń. Czyli podsumowując: pływak przepłynie łącznie 106 okrążeń w prawo i 106 w lewo a potem jeszcze 48 okrążeń w prawo. Razem da to 260 okrążeń. Z racji tego, że promień okręgu jest zmienny, co powoduje, że pokonywany dystans jest zmienny z każdym okrążeniem, to do pokonania 100 km potrzebne jest 260 okrążeń czyli o 100 wiecej niż w poprzedniej metodzie. Biłgoraj – Zalew Bojary – pływanie 100 km.

Dystans D okrążenia po okręgu o promieniu D = 2PiR, gdzie R = promień okręgu, w naszym przypadku jest to 100m, a 2*Pi = 6.28. Dystans okrążenia po okręgu 100m wynosi 628 m.
Jeśli lina nawija się na słup o promieniu r = 0,1 m, to podczas jednego okrążenia skraca się o 2Pir = 0,628 m. Biłgoraj – Zalew Bojary – pływanie 100 km.

Zadanie 3

Ciekawe zadanie powstaje, jeśli lina będzie się skracać za każdym razem nawijając się na poprzednie warstwy tworząc spiralę. W takiej spirali każde okrążenie jest krótsze o 0,628 m tworząc ciąg liczbowy. Do rozwiązanie tego zadania wykorzystaliśmy Google Gemini https://gemini.google.com , co przedstawia poniższy obrazek:

Równanie to można uprościć do następującej formy ( Biłgoraj – Zalew Bojary – pływanie 100 km )

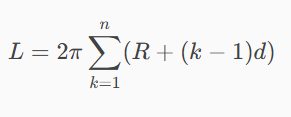
i następnie

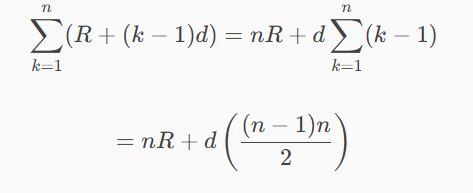
co po wymnożeniu daje równanie kwadratowe

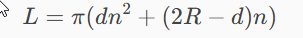
i następnie

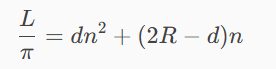
Równanie - Biłgoraj - Zalew Bojary - pływanie 100 km

W tej sytuacji mamy równanie kwadratowe typu ax^2 + bx + c =0. Używając formuły kwadratowej x = (−b ± pierwiastek kwadratowy z ( b2 − 4ac) ) / 2a, dostajemy: n = 160,43. Tak więc w takiej sytuacji pływak wykona 160 okrążenia na ciągle skracającej się linie. Biłgoraj – Zalew Bojary – pływanie 100 km

Dla miłośników Pythona, zadanie może być rozwiązane przy pomocy poniższej procedury. Biłgoraj – Zalew Bojary – pływanie 100 km.

def calculate_turns(rope_length, rope_thickness, bar_radius, shorten_per_turn, turns_per_layer, layer_increase):
    turns = 0
    while rope_length > 0:
        turns += 1
        rope_length -= shorten_per_turn
        if turns % turns_per_layer == 0:
            bar_radius += layer_increase / 2
            shorten_per_turn = 2 * 3.14 * (bar_radius + rope_thickness)
    return turns
# Given values
rope_length = 100  # meters
rope_thickness = 0.01  # meters (1 cm)
bar_radius = 0.1  # meters
shorten_per_turn = 0.628  # meters
turns_per_layer = 10
layer_increase = 0.02  # meters (2 cm)

# Calculate the number of turns
turns = calculate_turns(rope_length, rope_thickness, bar_radius, shorten_per_turn, turns_per_layer, layer_increase)

print(f"The swimmer can make {turns} turns before the rope ends.")

More python here

Biłgoraj – Zalew Bojary – pływanie 100 km

Pływania w dobrej sprawie – Biłgoraj – Zalew Bojary – pływanie 100 km

Artykuł opisuje niezwykłe wyzwanie wytrzymałościowe podjęte przez pływaka Damiana Błaszczyka, który postanowił przepłynąć 100 kilometrów w zbiorniku wodnym Zalew Bojary w Biłgoraju. Wydarzenie to, będące częścią inicjatywy „Na Fali Nadziei – Przekraczając Granice”, ma nie tylko sportowy, ale przede wszystkim charytatywny charakter. Celem tegorocznej edycji jest wsparcie Adasia Iwanejko, 12-letniego chłopca chorego na dystrofię mięśniową Duchenne’a. Zebrane środki mają pomóc w sfinansowaniu kosztownej terapii genowej w USA, której koszt przekracza 16 milionów złotych.

Matematyka pływania – modelowanie dystansu

Autor bloga przedstawia matematyczne modele opisujące, jak można przepłynąć 100 km w jednym zbiorniku. W pierwszym scenariuszu Damian pływa po idealnym okręgu, przymocowany do słupa liną o długości 100 metrów. Każde okrążenie ma wtedy około 628 metrów (obliczone ze wzoru na obwód koła: (2\pi r)). Aby osiągnąć 100 km, potrzeba 160 okrążeń, zmieniając kierunek co 10, by równomiernie obciążać ciało. Przy stałym tempie 4 km/h, całość zajęłaby około 25 godzin, choć wydarzenie przewiduje 48 godzin, co czyni cel realnym.

Realizm: lina nawijająca się na słup

Drugi scenariusz uwzględnia bardziej realistyczny aspekt – lina nawija się na słup, skracając z każdym okrążeniem promień pływania. Słup ma 20 cm średnicy, a lina 1 cm grubości. Po każdych 10 okrążeniach lina tworzy nową warstwę, zwiększając promień słupa. W efekcie każde kolejne okrążenie jest krótsze. Obliczenia pokazują, że Damian może wykonać 106 okrążeń w jednym kierunku, pokonując 37,7 km. Powtórzenie tego w przeciwnym kierunku daje kolejne 37,7 km. Aby osiągnąć 100 km, potrzeba jeszcze 48 dodatkowych okrążeń, co daje łącznie 260 okrążeń – o 100 więcej niż w pierwszym modelu.

Model spiralny – matematyczna elegancja

Trzeci model zakłada spiralne nawijanie liny, gdzie każde okrążenie jest krótsze o stałą wartość. Tworzy to ciąg arytmetyczny długości okrążeń. Korzystając z wzoru na sumę ciągu, autor oblicza, że potrzeba około 160,43 okrążeń, by osiągnąć 100 km. Model ten jest zbliżony do pierwszego, ale bardziej realistyczny i matematycznie elegancki.

Podsumowanie

Artykuł łączy sport, charytatywność i matematykę w inspirującą opowieść. Pokazuje nie tylko niezwykłe wyzwanie fizyczne, ale też to, jak matematyka może pomóc zrozumieć i zaplanować realne działania. Wydarzenie nad Zalewem Bojary to dowód ludzkiej wytrwałości i solidarności – każdy przepłynięty metr to krok ku nadziei dla chorego chłopca. Biłgoraj – Zalew Bojary – pływanie 100 km.

Biłgoraj – Zalew Bojary – pływanie 100 km

Zadanie 1. Biłgoraj – Zalew Bojary – pływanie 100 km

Zadanie 2

Zadanie 3

Pływania w dobrej sprawie – Biłgoraj – Zalew Bojary – pływanie 100 km